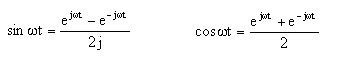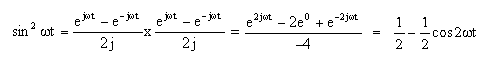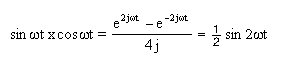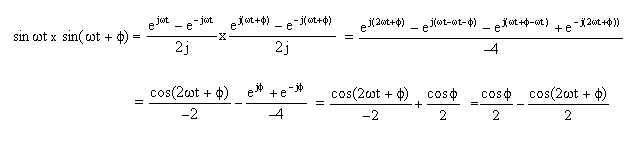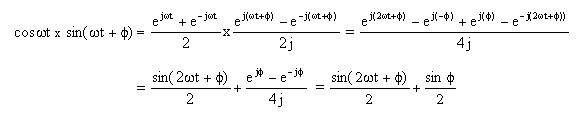QPSK

Prendendo i concetti prima esposti per la PSK il passo successivo e' assumere che il numero degli sfasamenti non e' limitato a due e che la portante del trasmettitore può subire qualunque cambiamento di fase. Quindi in uscita del modulatore si ha un segnale che può presentare un certo numero di sfasamenti. Per demodulare tale segnale lo si moltiplica con un segnale sinusoidale ad eguale frequenza ottenendo, dopo un filtraggio, un segnale di ampiezza proporzionale allo sfasamento. Se i possibili cambiamenti di fase della portante sono quattro si ha il caso del QPSK (quadra-phase-shift keying ). Cosi possono essere trasmessi 4 segnali diversi che corrisponde a  trasmettere due bit contemporaneamente. Questo vuol dire che si e' raddoppiata la banda della portante.
La dimostrazione di come la modulazione di fase e quindi la QPSK sono demodulate e' mostrata di seguito. La dimostrazione inizia dalla relazione di Eulero, da cui tutte le grandezza trigonometriche derivano. La relazione di Eulero e' la seguente:

Ovvero una sinusoide e una cosinusoide possono essere scritte come combinazione di esponenziali complessi. Moltiplicando la relazione del seno per se stesso si ottiene:

Dall'equazione 1, si può vedere che moltiplicando due onde sinusoidali assieme tra loro si ottiene in uscita una componente

con frequenza doppia rispetto a quella di ingresso e con un ampiezza dimezzata  e centrata su un offset  dc (1/2)
Nel caso reale questa situazione si verifica quando si utilizza un circuito di miscelazione come modulatore. In ingresso si hanno le due sinusoidi: la modulante e  la portante. In uscita si ha un segnale avente una componente a frequenza pari alla combinazione algebrica delle frequenze della portante e della modulante e una componente dc.
Allo stesso modo se si moltiplicano la quantità e si ha:

che da come uscita una componente in frequenza doppia rispetto all'ingresso e nessuna componente in continua.
E' lecito fare l'assunzione che, moltiplicando con una sinusoide con sfasamento , si ottenga una forma d'onda "demodulata" con una frequenza doppia rispetto a quella di ingresso e con una componente dc che varia in ampiezza in funzione in accordo con lo sfasamento f . Per dimostrare questo, di seguito sono mostrati alcuni calcoli:

Così, il risultato ottenuto prova la supposizione che una portante modulata in fase possa essere demodulata in una tensione di  variabile ottenuta moltiplicando la portante con un segnale sinusoidale, prodotto da un oscillatore locale, e filtrando la componente ad alta frequenza. Sfortunatamente lo spostamento della fase e' limitato a due quadranti; uno sfasamento di p /2 non può essere distinto da uno sfasamento di -p /2. Quindi, per decodificare in maniera accurata una modulazione di fase a quattro quadranti, bisogna moltiplicare il segnale modulato con una sinusoide e con una cosinusoide, filtrare le componenti in frequenza e ricostruire i dati. La dimostrazione di ciò, espandendo quanto esposto matematicamente prima, e' mostrato di seguito: