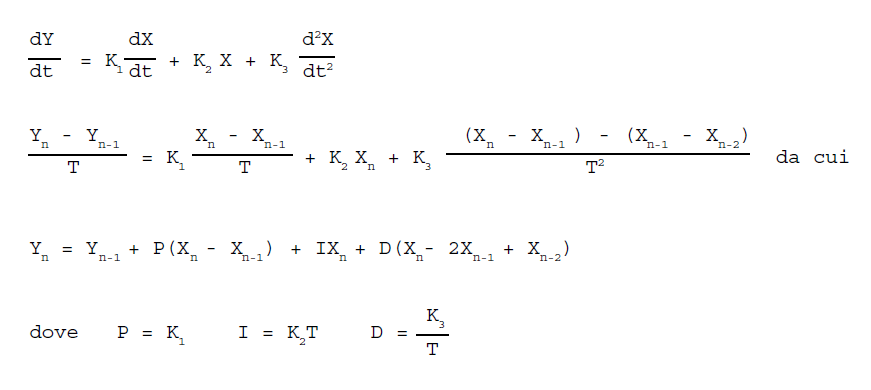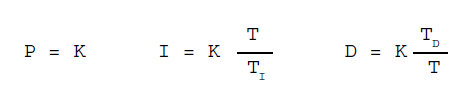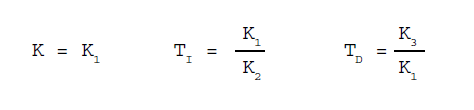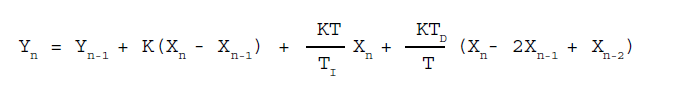PID & MICRO - 4

La realizzazione pratica di un sistema di regolazione ad anello chiuso con rete correttrice di tipo PID richiede normalmente una componentistica di tipo analogico; per esempio un effetto di tipo integrativo lo si ottiene inserendo nell'anello una rete ritardatrice costituita da un partitore RC (R in serie e C verso massa) capace di integrare nel tempo il valore dell'errore. Un effetto derivativo richiede invece una rete anticipatrice costituita da un partitore RC (C in serie e R verso massa) capace di lasciar passare le rapide variazioni dell'errore.
Disponendo di un sistema a microprocessore, capace di elaborare solo grandezze discrete, si richiede la conseguente discretizzazione della funzione PID; la funzione analogica viene aggiornata in modo digitalizzato e quindi simulata tramite software.
Derivando rispetto al tempo ambo i membri della precedente equazione, si ottiene la seguente forma discreta utilizzata per il calcolo della funzione PID:

Essendo una funzione discretizzata, è stato introdotto il tempo T di aggiornamento dell'equazione; questo è l'intervallo che intercorre tra due successivi aggiornamenti del valore dell'uscita Y della funzione. Conseguentemente i valori delle variabili X ed Y sono stati
considerati solo in tali istanti di campionamento e per questo indicati con n, n-1, n-2; il valore n si riferisce all'ultimo campionamento effettuato, n-1 al penultimo ed n-2 al terzultimo.
L'utilizzo di tale formula discretizzata consente di approssimare con sufficiente precisione l'equazione matematica continua riportata nel precedente paragrafo; è importante sottolineare che l'accuratezza della funzione è tanto più elevata quanto più i campionamenti sono
frequenti e quindi quanto più il tempo T di ripetizione dell'aggiornamento è piccolo. La discretizzazione si traduce infatti in un'approssimazione a gradini dell'andamento reale della variabile continua analogica; per la precisione, il valore medio della variabile discretizzata a gradini è ritardato di T/2 rispetto al vero andamento della variabile continua.
Una limitazione al desiderio di abbassare il tempo T, con lo scopo di ottenere le migliori prestazioni possibili, è dovuta all'impegno che l'aggiornamento dell'equazione richiede al microprocessore, in quanto essa richiede una certa mole di calcoli matematici. Si tratta quindi
di stabilire un tempo T tale da non costringere il microprocessore ad aggiornare l'equazione più frequentemente di quanto serva (in funzione della più o meno lentezza di variazione della variabile di ingresso X) ma, al tempo stesso, capace di far reagire prontamente la variabile Y alla variazione del segnale di errore X.

Il valore di tempo T, assieme ai tre parametri caratteristici P, I, D della funzione, costituiscono le uniche costanti da determinare per definire completamente l'algoritmo di calcolo: il valore di questi parametri dipende fortemente dal sistema controllato e esprime le
caratteristiche fisiche proprie dello stesso.
I parametri PID si possono ridefinire diversamente in funzione di grandezze più adatte ad individuare le caratteristiche fisiche di un sistema:

Dalle formule precedenti si deduce che per tale ridefinizione si è considerato:

Il valore K si dice costante di proporzionalità o guadagno proporzionale, il tempo TI tempo integrativo ed il tempo TD tempo derivativo. la costante K è espressa nel rapporto delle unità di misura di Y su X, mentre i tempi TI e TD sono normalmente espressi in secondi così come il tempo T di ripetizione dell'aggiornamento.
Con le nuove grandezze definite la formula per il calcolo discretizzato della funzione PID può essere così riscritta:

Si consideri che su un sistema a microprocessore può essere vantaggioso utilizzare unità di misura diverse da quelle più comuni allo scopo di eseguire operazioni solo su grandezze di tipo intero. Per esempio le costanti di tempo possono essere espresse in decimi di secondo, mentre la costante K può essere premoltiplicata per 1000 per considerarne tre cifre decimali pur utilizzando un valore intero. In tal caso occorrerà dividere tutta la parte incrementale (a destra del termine Yn-1) della formula per lo stesso fattore 1000 per aggiustarla alla nuova unità di misura di K. Si noti che l'utilizzo di unità di misura delle costanti di tempo diverse ma tra loro omogenee non richiede aggiustaggi della formula in quanto i termini contengono sempre rapporti di valori temporali. Infine per quanto riguarda i valori analogici di ingresso X e di uscita Y della formula si possono, con opportune scelte, considerare ancora solo numeri interi. Per esempio se la lettura della temperatura reale R è effettuata mediante un convertitore analogico/digitale a 8 bits dove lo stadio di amplificazione e offset del sensore sono stati tarati per fornire il valore 0-255 in corrispondenza a 0-100 gradi ed inoltre il set point S è impostabile da 0 a 100 gradi mediante il valore 0-255 di un secondo ingresso analogico connesso ad un potenziometro, non occorre convertire in gradi la lettura dei convertitori ma è possibile considerare le temperature espresse in questa nuova unità di misura intera.
Analogamente l'uscita Y normalmente corrisponde al valore 0-255 di una uscita analogica del microprocessore o di un circuito PWM a 8 bits.