OSCILLATORI - 8

Gli oscillatori a quarzo sfruttano l'effetto piezoelettrico per ottenere una elevata stabilita di frequenza. Si definisce stabilità di frequenza la variazione percentuale della frequenza del segnale prodotto da un oscillatore nell'intorno del valore nominale f_o. La relazione che esprime matematicamente la stabilità di frequenza e':

S% = 100 Df / f_o

Le cause della instabilità di frequenza sono molteplici, legate in particolare alle variazioni della temperatura, della tensione di alimentazione e del carico. L'influenza del carico può essere minimizzata inserendo tra l'oscillatore e l'utilizzatore uno stadio separatore (buffer), costituito ad esempio da un amplificatore nella configurazione a inseguitore. L'impiego di tensioni di alimentazione fortemente stabilizzate, di componenti resistivi a basso coefficiente di temperatura e di circuiti filtranti ad alta selettività, consente di raggiungere valori della stabilita di frequenza dell'ordine dello 0,01%, che tuttavia non sono sufficienti per molte applicazioni nelle quali sono richieste frequenze di lavoro rigorosamente costanti.Valori di stabilita nettamente superiori, dell'ordine di 10e-5 ÷ 10e-7 (ovvero di 10e-1÷  10e-4 ppm, parti per milione), si ottengono inserendo nel circuito fíltrante dell'oscillatore un cristallo piezoetettrico, cioè una lamina di quarzo compresa fra due elettrodi.
Elettricamente il cristallo piezoelettrico presenta due frequenze di risonanza, come risulta dal circuito equivalente rappresentato in figura 13

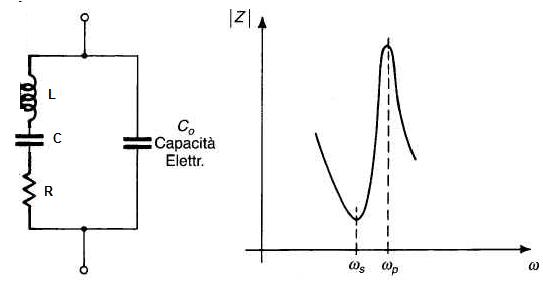
Fig. 13 – a) Circuito equivalente di un cristallo piezoelettrico; b) caratteristica di impedenza

/p>

I valori di L, C, R  dipendono dalle caratteristiche meccaniche del cristallo e precisamente dalle sue dimensioni (maggiore è la massa, più bassa e' la frequenza di vibrazione), dal coefficiente di elasticità del materiale e dall'attrito interno (perdite per isteresi meccanica). Il valore di C_o è invece quello della capacità elettrica fra i due elettrodi metallici della lamina. Ne risulta un circuito serie-parallelo con una risonanza serie frequenza w_s per cui si ha:

w_s² LC = 1 

ed una risonanza parallelo alla frequenza w_p

w_p² LC = 1   

w_p  >  w_s

In corrispondenza di w_s  l'impedenza e' minima ( risonanza di corrente), mentre in corrispondenza di w_p  e' massima (risonanza di tensione), come indicato nel grafico di figura 13. A tali frequenze, il valore di R nel circuito equivalente risulta piccolo in confronto alla reattanza della L, per cui il fattore di risonanza Q ha un valore elevatissimo dell'ordine di 10e³  ÷ 10e⁶. Da qui la grande selettività del circuito e l'alta stabilita di frequenza che ne deriva per gli oscillatori a quarzo. Come si vede, le due frequenze di risonanza sono molto vicine fra loro. In corrispondenza di w_s e di w_p l'impedenza del cristallo è, per definizione, puramente ohmica; tra le due frequenze è invece di tipo induttivo, mentre al disotto di w_s e al disopra di w_p è di tipo capacitivo.